de la Tierra por el método
de Eratóstenes
UNA ACTIVIDAD PARA SECUNDARIA

Eratóstenes de Cirene (276 a. C. - 194 a. C.) fue un cartógrafo, físico y matemático de la época helenística y director de la famosa Biblioteca de Alejandría, situada en el norte de Egipto, que calculó la circunferencia de la Tierra con uno de los experimentos más famosos de la historia de la física: tomaba en cuenta el sol cenital en un punto del planeta y el ángulo de la sombra que producía un cuerpo en otro punto, alejado algunos cientos de kilómetros del primero. La siguiente actividad reproduce el método de Eratóstenes para calcular la circunferencia del planeta para dos valores diferentes, lo que servirá como guía para que grupos escolares de secundaria la lleven a cabo. Esta actividad guarda relación con temas de física, matemáticas, geografía e historia.
En la Grecia Antigua, antes de la muerte del conquistador Alejandro Magno (356 a. C. - 323 a. C.), lo que da inicio al periodo helenístico, ya existía la idea de la esfericidad de la Tierra, por lo que era común que muchos estudiosos asimilaran que el planeta era una gran esfera en cuya superficie externa estaban todas las cosas, animales, plantas y seres humanos. Entre esos pensadores se encontraban Pitágoras (569 a. C. - 475 a. C.) y Platón (387 a. C. - 347 a. C.) (Meléndez, 2019).
La principal prueba que se tenía para creer que la Tierra era esférica era la sombra que proyectaba la Tierra en la Luna durante los eclipses, ya que, independientemente de la posición de ambos cuerpos, la sombra siempre se apreciaba circular, lo que coincide con cualquier sombra que proyecta una esfera. Esta prueba, indirecta, no es concluyente, pero sí proporciona un fuerte indicio de la forma de nuestro planeta.
Eratóstenes, que vivía en Alejandría y que era director de su biblioteca y museo –el equivalente a un centro de investigación moderno–, compartía esta visión y se imaginaba que la luz del Sol incidía en la Tierra, como se muestra en la siguiente figura:

Figura 1. Rayos solares inciden de forma paralela en el planeta
El sabio helenista creía que los rayos del Sol viajaban e incidían sobre la Tierra de forma paralela. Así, alguien en el punto A de la figura 2, vería el Sol exactamente arriba de él, en el cenit, y otra persona en el punto B lo vería ligeramente inclinado debido a la curvatura de la superficie terrestre:
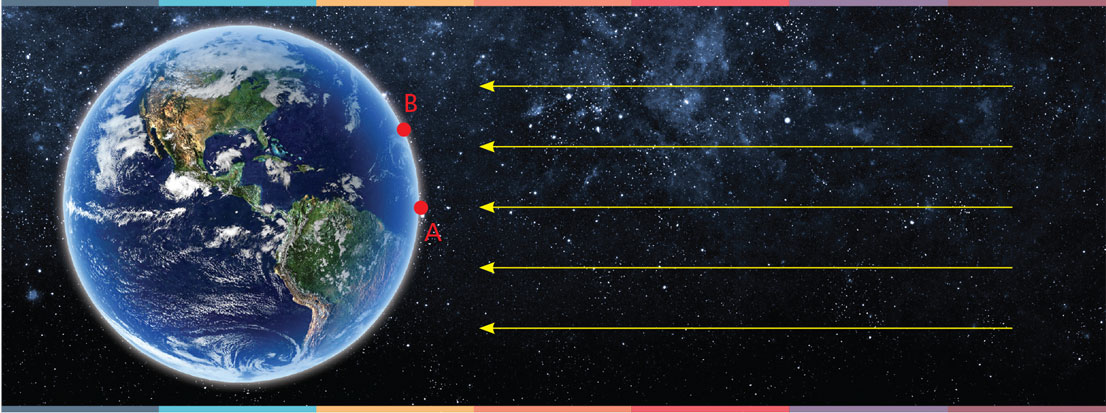
Figura 2. Debido a la curvatura del planeta, lo posición del Sol se ve diferente en dos puntos de su superficie alejados uno del otro
|
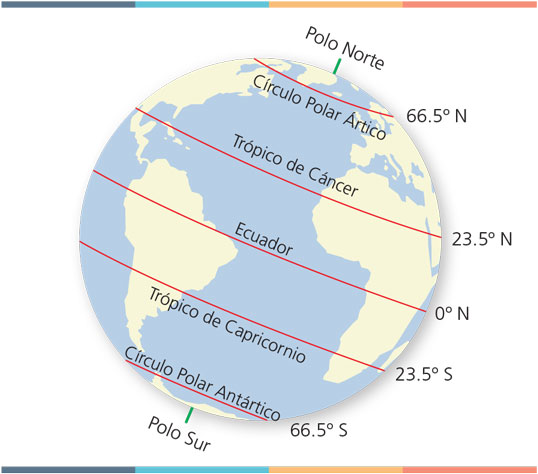
Hay que tener claro que el Sol en el cenit se presenta solamente en la superficie del planeta delimitada entre los trópicos de la Tierra: el de Cáncer al norte y el de Capricornio al sur. Los trópicos, recordemos, son paralelos, líneas diferentes a los meridianos que cruzan los polos. |
|
|
Figura 3. El trópico de |
Lo anterior se debe a la inclinación del eje de rotación del planeta y al movimiento de traslación de éste alrededor del Sol, como se aprecia a continuación:
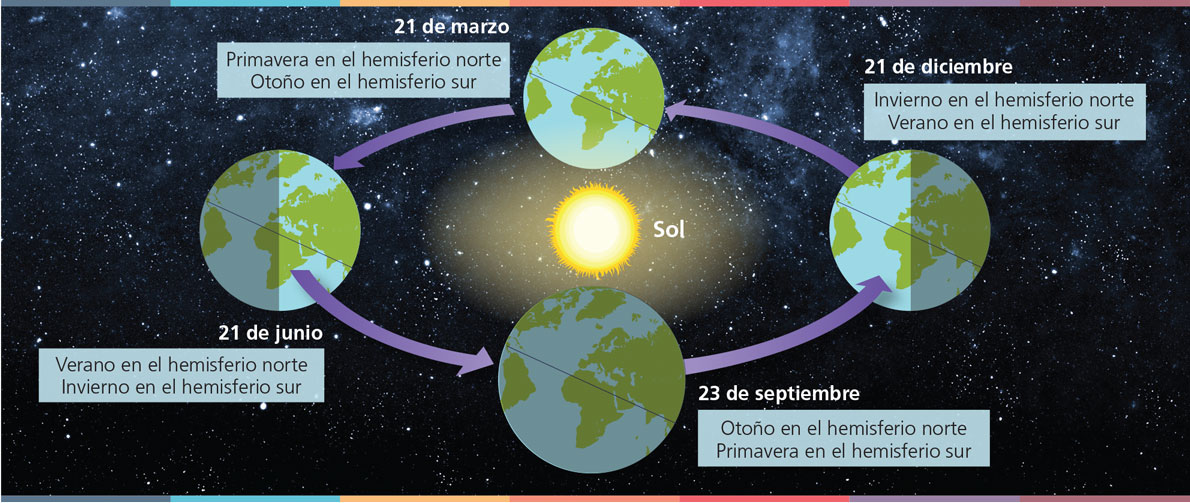
Figura 4. El sol cenital se aprecia en distintos puntos del planeta a lo largo del año
Recordemos que la inclinación del eje de rotación de la Tierra es de poco más de 23°, lo que indica los grados a los que se encuentran los trópicos. Si la Tierra tuviera un eje de rotación de, por ejemplo, 40°, los trópicos y los puntos del planeta por donde el Sol se presenta cenitalmente se ubicarían hasta los paralelos que coincidan con este valor.
Específicamente, en cada punto de la superficie entre los trópicos, el sol cenital pasa dos veces por año, como lo sabía Eratóstenes en el siglo III a. C., lo que le ayudó a determinar el tamaño de la circunferencia de la Tierra.
Si leemos al bien documentado Garfield (2013) en su libro En el mapa, entenderemos el método utilizado por el famoso bibliotecario de Alejandría:
Eratóstenes había observado que, en el solsticio de verano, los rayos del sol inciden perpendicularmente sobre la ciudad de Siena (la moderna Asuán), a las orillas del Nilo, como demostraba su reflejo en un profundo pozo a mediodía. Sabía, por el tiempo que se tardaba en hacer el viaje en camello entre las dos ciudades, que Siena se hallaba aproximadamente a 5000 estadios (unos 800 kilómetros) directamente al sur de Alejandría (en el meridiano principal que había situado sobre Rodas). Midiendo el ángulo de elevación del sol desde la Gran Biblioteca en ese mismo momento (7°), trazó la circunferencia de la Tierra. Suponiendo que la Tierra era esférica y que tenía 360°, la diferencia de 7° entre los 800 kilómetros equivalía a 1/50 de toda la esfera. Por tanto, Eratóstenes declaró que la circunferencia de la Tierra tenía 250 000 estadios (algo más de 40 000 kilómetros), cálculo que después elevó a 252 000 estadios para que la cifra fuera divisible entre 60.
Dicho de otra manera, Eratóstenes realizó lo siguiente:
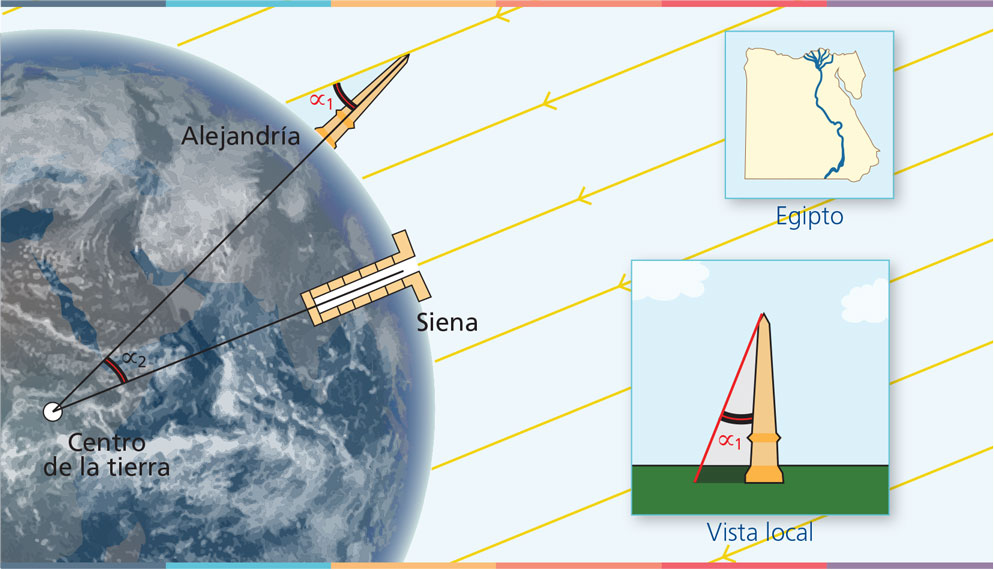
Midió el ángulo de una sombra en Alejandría, su ciudad, en el mismo momento en que se encontraba el sol cenital en Siena, la actual ciudad de Asuán. Este ángulo es el mismo que se forma teniendo como vértice el centro de la Tierra y las dos ciudades, como se ilustra aquí:
Figura 5. El |
 |
Además, Eratóstenes conocía la distancia entre las dos ciudades, que era de unos 800 kilómetros. Por lo que a partir de este dato…
¡Utilizó una regla de 3 simple para calcular la circunferencia del planeta!, de la siguiente manera:

Así, sencillo, lo que demuestra la inteligencia del nacido en Cirene.
En el cálculo de la circunferencia de la Tierra por el método de Eratóstenes se requiere conocer la distancia entre dos puntos geográficos, que de preferencia, estén separados por una distancia considerable para que el ángulo formado en uno de ellos por la sombra sea lo suficientemente grande. Con distancias mayores a los 400 kilómetros ya se pueden obtener datos que proporcionen resultados confiables.
Una idea extendida para el cálculo de la superficie de la Tierra por este método dice que los dos puntos geográficos por considerar deben estar en el mismo meridiano, o muy cerca de él, pero esto no es correcto debido a la simetría esférica del planeta. Por ello, es suficiente con que en uno de ellos se encuentre el sol cenital sin importar si el otro se encuentra o no en el mismo meridiano.
Partiendo de lo anterior, en el caso de la práctica que realizamos para este artículo, contactamos a dos personas que viven en dos lugares diferentes para asegurar, por lo menos, un dato correcto por si en alguna ciudad se nublaba: Violeta Márquez-Cruz, que vive en Quebec (Canadá), y Daniela Tarhuni, en Mérida, Yucatán (México). Ambas midieron la sombra de un palo de escoba para determinar el ángulo en el mismo momento del paso del sol cenital por la casa del autor de este artículo, en Coatepec, Veracruz (México), exactamente a las 13:33 horas del 25 de julio de 2021.
Coatepec sería la Siena de Eratóstenes, y Quebec o Mérida, la Alejandría (ver fig. 6).
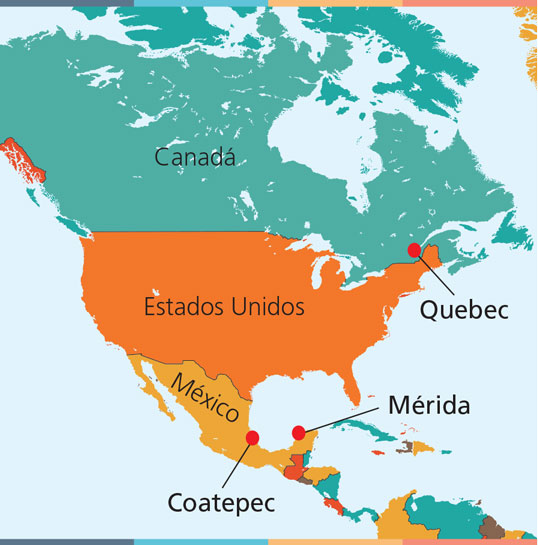
Figura 6. Posición de las 3 ciudades del experimento moderno para el cálculo de la circunferencia de la Tierra
Ahora bien, el equivalente de medir la distancia entre dos ciudades trasladándose en camello en la época de Eratóstenes sería, actualmente, hacerlo en un avión, cosa que no fue posible. Así que nos tomamos la licencia de obtener ese dato de la página TuTiempo.net, donde al establecer las coordenadas de dos puntos de la Tierra se proporciona su separación considerando la curvatura del planeta. Por supuesto que con esta misma página es posible conocer la circunferencia buscada, lo que le quitaría cualquier interés a esta actividad. Lo único que pretendíamos era partir con los datos equivalentes que tuvo Eratóstenes.
Como no se nubló en Quebec ni en Mérida, obtuvimos dos resultados.

Figura 7. Tamaño de las sombras: (1) Coatepec, sol cenital; (2) Quebec; y (3) Mérida en el mismo momento
Ángulo medido en Quebec a partir de la longitud de una cuerda y del largo de la sombra: 34.28° (como se aprecia en la figura 7):
Distancia Coatepec-Quebec: 3878.93 km
Circunferencia calculada (1):
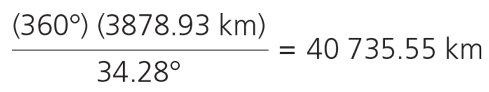
Ángulo medido en Mérida a partir de la longitud del palo y del largo de la sombra: 7.18° (como se aprecia en la figura 7).
Distancia Coatepec-Mérida: 784.58 km
Circunferencia calculada (2):
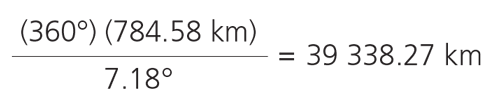
Si tomamos en cuenta que la circunferencia de la Tierra es de 40 075 km, ambos resultados son muy buenos.
Eratóstenes, ¡genio!

Figura 8. Circunferencias calculadas en la actividad
Como se puede apreciar en la mayoría de los mapas, el trópico de Cáncer divide en dos regiones al país (fig. 9), por lo que, en toda la superficie de Baja California, Sonora, Chihuahua, Coahuila, así como buena parte de Nuevo León, Baja California Sur, Sinaloa, Durango, Tamaulipas y algunas regiones de Zacatecas y San Luis Potosí no se presenta el sol cenital ningún día del año, lo que no es impedimento para efectuar esta actividad, como se plantea a continuación.
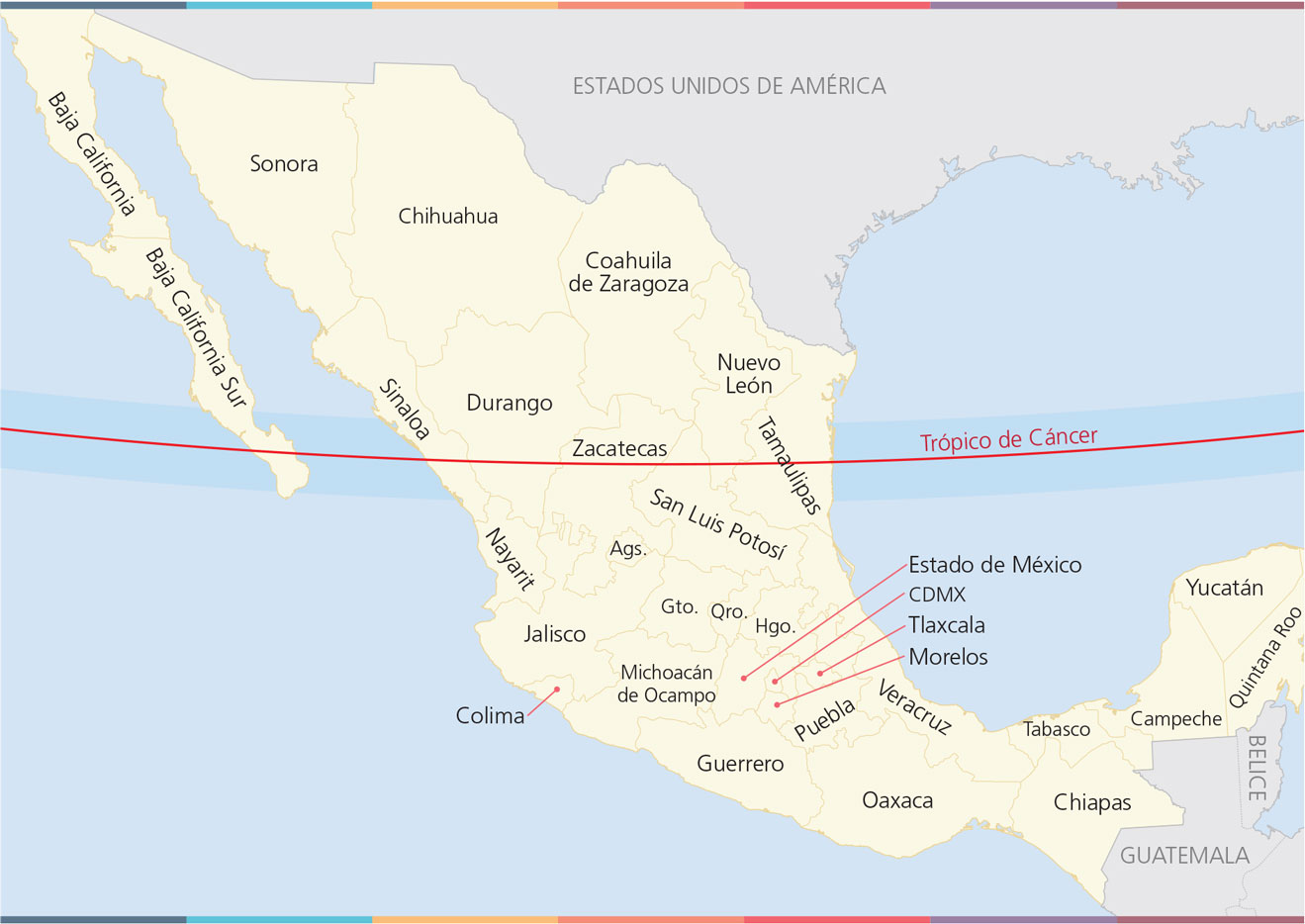
Figura 9. El trópico de Cáncer divide a México en dos regiones
Propóngale a su grupo que investigue el nombre de una ciudad o poblado de América (incluyendo México) donde vaya a presentarse el sol cenital, y con la ayuda de usted establezcan contacto con alguna escuela de su mismo nivel educativo. Existen varias páginas donde proporcionan la fecha del paso del Sol por el cenit dadas las coordenadas, como SunEarthTools.com, y
Inviten a los alumnos, profesores o directivos de esa escuela a que realicen en conjunto con ustedes esta actividad, donde ellos serán Siena y ustedes Alejandría. Es decir, en el momento en que se presente el sol cenital en la escuela que contactaron, ustedes medirán la sombra de un palo de escoba en posición vertical (o cualquier objeto alargado) para determinar el ángulo que sustenta a las dos escuelas (o ciudades) con el centro de la Tierra en el vértice.
Con el procedimiento que ya se planteó, determinen la circunferencia de la Tierra.
Si en su ciudad sí se presenta el sol cenital en algún momento del año, también deberán contactar alguna escuela que se encuentre a varios cientos de kilómetros de distancia para proponerle efectuar de manera conjunta esta actividad. Ahora ustedes serán Siena, y la otra escuela, Alejandría.
Desde luego, si alguien del salón de clases conoce a alguna persona que viva a varios cientos de kilómetros de la escuela y que pueda ayudarles, pueden recurrir a ella.
En las encuestas que suelen realizarse entre especialistas sobre los experimentos más bellos de la física, comúnmente aparece el que realizó Eratóstenes de Cirene, en el siglo III a. C., porque, coincide la mayoría, se trata de una idea asombrosa y reveladora demostrada con gran sencillez, ya que su resultado nos muestra, ni más ni menos, las dimensiones del planeta que habitamos. Por ello, reproducirla en el lugar donde se viva daría un sentido de pertenencia histórica, pero también de comprensión física, matemática y geográfica sobre nuestro planeta, propósitos fundamentales de la escuela.♦
GARFIELD, Simon (2013). En el mapa. Taurus.
MELÉNDEZ, Haydeé (2019). Cómo los antiguos griegos sabían que la Tierra era redonda. Soltekonline. https://blog.soltekonline.com/como-los-antiguos-griegos-sabian-que-la-tierra-era-redonda/ Ir al sitio
SunEarthTools.com (s. f.). https://www.sunearthtools.com/dp/tools/pos_sun.php?lang=es Ir al sitio
TuTiempo.net. (s. f.). https://www.tutiempo.net/ Ir al sitio
Notas
* Físico por la UNAM, maestro en ciencias por el IPN y fotógrafo. Profesor en la Universidad Veracruzana. Escribe sobre ciencia en varios medios y en sus redes sociales, como <www.facebook.com/josemanuel.posada.5>.- Imagen inicial: www.alamy.es
- Figura 1 a 5: Correo del Maestro con imágenes de Shutterstock
- Figura 6: Correo del Maestro con imágenes
- Figura 7: José Manuel Posada de la Concha
- Figura 8: www.google.com.mx/maps
- Figura 9: Correo del Maestro con imágenes
CORREO del MAESTRO • núm. 311 • Abril 2022